HOUSTON JOURNAL OF
MATHEMATICS
Electronic Edition Vol. 50, No. 3, 2024
Editors: D. Bao (San Francisco, SFSU), S. Berhanu (Temple), D. Blecher
(Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers),
B. Dacorogna (Lausanne), M.
Gehrke (LIAFA, Paris7), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori
(Matsue, Shimane), W. B. Johnson (College Station), H. Koivusalo (Bristol), M. Marsh (Sacramento), M. Rojas (College Station),
Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and A. Haynes (Houston)
Houston Journal of Mathematics
Contents
Guo-Shuai Mao, Department of Mathematics, Nanjing University of Information Science
and Technology, Nanjing 210044, People’s Republic of China (maogsmath@163.com), and
Lei Shi, Department of Mathematics, Nanjing University of Information Science and
Technology, Nanjing 210044, People’s Republic of China (1960991228@qq.com).
Congruence properties for the quadrinomial coefficients, pp. 497–508.
ABSTRACT. In this paper, we mainly obtain some congruence properties for
the quadrinomial coefficients, one of which is analogous to the Wolstenholme’s
theorem. The quadrinomial coefficient is defined by the coefficient of xk in the
polynomial expansion of (1 + x + x2 + x3)n, where n and k are nonnegative integers.
Spencer Chapman, Mathematics Department, Trinity University, San Antonio, TX
78212 (schapma3@trinity.edu), Eli B. Dugan, Mathematics and Statistics Department,
Williams College, Williamstown, MA 01267 (ebd3@williams.edu), Shadi Gaskari,
Mathematics Department, San Diego State University, San Diego, CA 92182
(shgaskari@gmail.com), Emi Lycan, Mathematics Department, San Diego State
University, San Diego, CA 92182 (ronlycan1250@gmail.com), Sarah Mendoza De La
Cruz, Mathematics Department, University of Texas at Austin, Austin, TX 78712
(sarahpaolam11@gmail.com), Christopher O’Neill, Mathematics Department, San
Diego State University, San Diego, CA 92182 (cdoneill@sdsu.edu), and Vadim
Ponomarenko, Mathematics Department, San Diego State University, San Diego, CA
92182 (vponomarenko@sdsu.edu).
Some asymptotic results on p-lengths of factorizations for numerical semigroups and
arithmetical congruence monoids, pp. 509–523.
ABSTRACT. A factorization of an element x in a monoid (M,⋅) is an expression of x of
the form x = u1z1 ukzk for irreducible elements u1,…,uk ∈ M, and the length of such a
factorization is z1 +
ukzk for irreducible elements u1,…,uk ∈ M, and the length of such a
factorization is z1 +  + zk. We introduce the notion of p-length, a generalized notion of
factorization length obtained from the ℓp-norm of the sequence (z1,…,zk), and present
asymptotic results on extremal p-lengths of factorizations for large elements of
numerical semigroups (additive submonoids of ℤ≥0) and arithmetical congruence
monoids (certain multiplicative submonoids of ℤ≥1). Our results, inspired by
analogous results for classical factorization length, demonstrate the types of
combinatorial statements one may hope to obtain for sufficiently nice monoids, as
well as the subtlety such asymptotic questions can have for general monoids.
+ zk. We introduce the notion of p-length, a generalized notion of
factorization length obtained from the ℓp-norm of the sequence (z1,…,zk), and present
asymptotic results on extremal p-lengths of factorizations for large elements of
numerical semigroups (additive submonoids of ℤ≥0) and arithmetical congruence
monoids (certain multiplicative submonoids of ℤ≥1). Our results, inspired by
analogous results for classical factorization length, demonstrate the types of
combinatorial statements one may hope to obtain for sufficiently nice monoids, as
well as the subtlety such asymptotic questions can have for general monoids.
Nanhui Hu, Department of Mathematics, Shantou University, Shantou 515063,
Guangdong, P. R. China; Department of Mathematics, Jiaying University, Meizhou
514015, Guangdong, P. R. China (hunhjyu@163.com), and Songxiao Li, Department of
Mathematics, Shantou University, Shantou 515063, Guangdong, P. R. China
(jyulsx@163.com).
Closure in the logarithmic Bloch-type norm of Dirichlet-Morrey spaces, pp.
525–542.
ABSTRACT. Two characterizations for the closure of Dirichlet-Morrey spaces in the
logarithmic Bloch-type spaces are given in this paper. In particular, we get a new
characterization for the spaces 𝒞ℬ(H2 ∩ℬ) and 𝒞ℬ(BMOA), respectively. Furthermore,
we obtain a criterion for an interpolating Blaschke product to be in the closures.
Guo-Shuai Mao, School of Mathematics and Statistics, Nanjing University of
Information Science and Technology, Nanjing 210044, People’s Republic of China
(maogsmath@163.com), and Hao Pan, School of Applied Mathematics, Nanjing
University of Finance and Economics, Nanjing 210023, People’s Republic of China
(haopan79@zoho.com).
On the Atkin-Swinnerton-Dyer type congruences for some sequences arising from
Calabi-Yau equations, pp. 543–558.
ABSTRACT. In this paper, we show some supercongruences for the coefficients
{An}n=0,1,2,… of the analytic solution y0(z) = ∑
n=0∞Anzn to the Calabi-Yau type
equations Dy = 0 normalized by the condition y0(0) = A0 = 1, where D is a 4th-order
linear differential operator.
Mabud Ali Sarkar, Department of Mathematics, The University of Burdwan,
Burdwan 713104, India (mabudji@gmail.com), and Absos Ali Shaikh,
Department of Mathematics, The University of Burdwan, Burdwan 713104, India
(aashaikh@math.buruniv.ac.in).
On the image of p-adic logarithm on principal units, pp. 559–591.
ABSTRACT. The p-adic logarithm appears in many places in number theory. Therefore,
a comprehensive description of the image of the p-adic logarithm would be beneficial. In
particular, it is important to figure out the image of 1 + 𝔪K, where K denotes an
algebraic extension of ℚp and 𝔪K represents its maximal ideal. If the ramification
index of K is strictly less than p − 1, then it is known that the p-adic logarithm
serves as a bijection from 1 + 𝔪K to 𝔪K. If the ramification index is equal to or
greater than p − 1, then the p-adic logarithm is no longer a bijection, and the
situation is more complicated. Our main result is the computation of log p(1 + 𝔪K)
in two distinct cases: first, when K = ℚp(ζp), a totally ramified p-cyclotomic
extension of ℚp with a ramification index of p − 1; and second, when K is a
quadratic extension of ℚ2, characterised by a ramification index of either 1
or 2. As an application, we compute the normalised p-adic regulator of the
number field ℚ(ζp) by utilising the image of the p-adic logarithm on the units.
Lin Hu, School of Mathematical Sciences, Chongqing Normal University, Chong-qing,
401331, P. R. China (2840788320@qq.com), Rebecca Smith, The University of
Newcastle, Callaghan 2308, NSW, Australia (Rebecca.Smith@newcastle.edu.au), and
Zhenliang Zhang, School of Mathematical Sciences, Chongqing Normal University,
Chongqing, 401331, P. R. China (zhliang_zhang@163.com).
Geometric mean of Lüroth digits in arithmetic progressions, pp. 593–626.
ABSTRACT. This paper explores the Hausdorff dimension analysis of the sets of real
numbers for which the products of partial quotients in Lüroth expansion satisfy certain
growth conditions. That is, for any x ∈ (0,1], let [d1(x),d2(x),…] denote its Lüroth
expansion. Let Ψ : ℕ → (1,∞) be any function, we establish the Hausdorff dimension of
the set:
Ef(Ψ) := 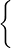 x ∈ (0,1] : x ∈ (0,1] : | 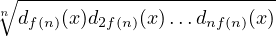 ≥ Ψ(n) ≥ Ψ(n) | |
|
| 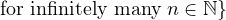 , , | | |
where f(n) := cn + t be a linear function, c ∈ ℕ and t ∈ ℤ≥0. It is to be noted that
when f(n) is a constant, the Hausdorff dimension stays the same irrespective of the value
of the constant. The Hausdorff dimension increases as c increases, whereas, t does not
impact the dimension.
Guodong Hua, School of Mathematics and Statistics, Weinan Normal University,
Weinan, Shaaxi Province, China 714099; Research Institute of Qindong
Mathematics, Weinan Normal University, Weinan, Shaaxi Province, China 714099
(gdhuasdu@163.com).
Weighted Erdős-Kac type theorems for higher moments of cusp form coefficients in short
intervals, pp. 627–660.
ABSTRACT. Let f be a normalized primitive holomorphic Hecke eigenform of even
integral weight κ for the full modular group Γ = SL(2, ℤ), and denote by λf(n) its n-th
Fourier coefficient. In this paper, we establish weighted Erdős-Kac type theorems for the
higher power moments of λf(n) in short intervals, by using the generalized
Selberg-Delange method developed in recent decades. We also establish the asymptotic
formulae for the same higher moments of λf(n) with prescribed number of prime
divisors in short intervals. By analogy, we also obtain the similar results for
the Fourier coefficients associated to two distinct cuspidal Hecke eigenforms.
Zhuo Chen, Department of Mathematics, School of Mathematical and Physical
Sciences, University of Sussex, BN1 9QH Brighton, United Kingdom, and Michael
Melgaard, Department of Mathematics, School of Mathematical and Physical Sciences,
University of Sussex, BN1 9QH Brighton, United Kingdom (m.melgaard@sussex.ac.uk).
Energy-localized Egorov theorem for matrix-valued Schrödinger operator without
Cordes’s hyperbolicity condition, pp. 661–697.
ABSTRACT. We establish a semi-classical Egorov type theorem for a matrix-valued
Schrödinger operator, frequently arising in important applications, which does not satisfy
typically imposed hypotheses, e.g., Cordes’s hyperbolicity condition. The proof combines
a number of new ideas and the techniques involve h-pseudodifferential operator calculus,
Riesz projection formula, energy localization, and detailed study of the Heisenberg
equations on symbol level using the time-dependent Schrödinger equation to justify an
auxiliary localized initial condition which allows for a detailed analysis of the
Hamiltonian flow and the derivation of key estimates for the solutions to new auxiliary
Heisenberg equations.
Qing Zhang, Anhui International Studies University, Anhui, 231201, China
(zhangqing20241212@163.com), and Akbar Jahanbani, Department of Mathematics,
Azarbaijan Shahid Madani University, Tabriz, Iran (akbar.jahanbani92@gmail.com).
Modified Sombor index of graphs with a given girth, pp. 699–707.
ABSTRACT. The modified Sombor index of a graph G is defined as mSO(G)
= ∑
uv∈E(G) , where du is the degree of the vertex u in G. In this paper, the
minimum and maximum values of the modified Sombor index for connected
graphs with girth l(l ≥ 3) are determined. Moreover, we obtain lower and upper
bounds for the modified Sombor index which depend on the girth of a graph.
, where du is the degree of the vertex u in G. In this paper, the
minimum and maximum values of the modified Sombor index for connected
graphs with girth l(l ≥ 3) are determined. Moreover, we obtain lower and upper
bounds for the modified Sombor index which depend on the girth of a graph.
Ofelia T. Alas, Instituto de Matemática e Estatística, Universidade de São Paulo,
Caixa Postal 66281, 05314-970 São Paulo, Brasil (alas@ime.usp.br), L. Enrique
Gutiérrez-Domínguez, Departamento de Matemáticas, Universidad Autónoma
Metropolitana, Unidad Iztapalapa, Avenida San Rafael Atlixco, #186, Apartado Pos-tal
55-532, 09340, México, D.F., México (luenriquegudo@gmail.com), Lucia R.
Junqueira, Instituto de Matemática e Estatística, Universidade de São Paulo, Caixa
Postal 66281, 05314-970 São Paulo, Brasil (lucia@ime.usp.br), and Richard G.
Wilson, Departamento de Matemáticas, Universidad Autónoma Metropolitana, Unidad
Iztapalapa, Avenida San Rafael Atlixco, #186, Apartado Postal 55-532, 09340, México,
D.F., México (rgw@xanum.uam.mx).
Maximality and productivity of the weak Lindelöf property, pp. 709–723.
ABSTRACT. Necessary conditions are given in order that a topology be maximal with
respect to being weakly Lindelöf and preservation of the weak Lindelöf, the almost
Lindelöf and the weak linearly Lindelöf properties under products is studied.
Zhangyong Cai, Center for Applied Mathematics of Guangxi (Nanning Normal
University), College of Mathematics and Statistics, Nanning Normal University, Nanning
530100, P.R. China (zycaigxu2002@126.com), and Shou Lin, Institute of Mathematics,
Ningde Normal University, Ningde 352100, P.R. China (shoulin60@163.com).
A question on countable tightness of free Abelian paratopological groups, pp.
725–732.
ABSTRACT. This paper continues to study the countable tightness of free
Abelian paratopological groups. An open problem is whether the free Abelian
paratopological group AP(X) on a metrizable space X has countable tightness if the
subspace X′ consisting of all non-isolated points in X is separable. In this paper,
around the above problem, it is established that if X is a metrizable space with
only finitely many non-isolated points, then AP(X) has countable tightness.
Fang Liu, Institute of Mathematics, Ningde Normal University, Ningde, Fujian 352100,
P.R. China (58451372@qq.com), Shou Lin, Institute of Mathematics, Ningde
Normal University, Ningde, Fujian 352100, P.R. China (shoulin60@163.com),
Xin Liu, Institute of Mathematics, Ningde Normal University, Ningde, Fujian
352100, P.R. China (liuxintp@126.com), and Xiangeng Zhou, Institute of
Mathematics, Ningde Normal University, Ningde, Fujian 352100, P.R. China
(56667400@qq.com).
The symmetrizability in weak topological groups with ideal continuity, pp.
733–750.
ABSTRACT. A mapping which preserves ideal convergence of sequences between
topological spaces is precisely an ℐsn-continuous mapping. Based on ℐsn-continuity, in this
paper we consider some classes of weak topological groups, discuss the symmetrizability
of weak ℐsn-topological groups, and define and study quasi-ℐ-sn-symmetrizable spaces
as a common generalization of symmetrizable spaces and quasi-developable
spaces.
Let ℐ be an admissible ideal on the set ℕ of natural numbers. The following main
results are obtained.
(1) Every ℐ-sn-symmetrizable para-ℐsn-topological group is an ℐ-sn-develop-able
space.
(2) Every ℐsn-Baire, quasi-ℐ-sn-symmetrizable para-ℐsn-topological group is an
ℐsn-topological group.
These not only generalize some results related to the symmetrizability in weak
topological groups, but also present a version in topological algebra using the notion of
ideal convergence.
 ukzk for irreducible elements u1,…,uk ∈ M, and the length of such a
factorization is z1 +
ukzk for irreducible elements u1,…,uk ∈ M, and the length of such a
factorization is z1 +  + zk. We introduce the notion of p-length, a generalized notion of
factorization length obtained from the ℓp-norm of the sequence (z1,…,zk), and present
asymptotic results on extremal p-lengths of factorizations for large elements of
numerical semigroups (additive submonoids of ℤ≥0) and arithmetical congruence
monoids (certain multiplicative submonoids of ℤ≥1). Our results, inspired by
analogous results for classical factorization length, demonstrate the types of
combinatorial statements one may hope to obtain for sufficiently nice monoids, as
well as the subtlety such asymptotic questions can have for general monoids.
+ zk. We introduce the notion of p-length, a generalized notion of
factorization length obtained from the ℓp-norm of the sequence (z1,…,zk), and present
asymptotic results on extremal p-lengths of factorizations for large elements of
numerical semigroups (additive submonoids of ℤ≥0) and arithmetical congruence
monoids (certain multiplicative submonoids of ℤ≥1). Our results, inspired by
analogous results for classical factorization length, demonstrate the types of
combinatorial statements one may hope to obtain for sufficiently nice monoids, as
well as the subtlety such asymptotic questions can have for general monoids.
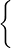
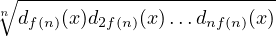
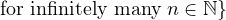
 , where
, where