HOUSTON JOURNAL OF
MATHEMATICS
Electronic Edition Vol. 50, No. 4, 2024
Editors: D. Bao (San Francisco, SFSU), S. Berhanu (Temple), D. Blecher
(Houston), B. G. Bodmann (Houston), H. Brezis (Paris and Rutgers),
B. Dacorogna (Lausanne), M.
Gehrke (LIAFA, Paris7), R. M. Hardt (Rice), S. Harvey (Rice), A. Haynes (Houston), Y. Hattori
(Matsue, Shimane), W. B. Johnson (College Station), H. Koivusalo (Bristol), M. Marsh (Sacramento), M. Rojas (College Station),
Min Ru (Houston), S.W. Semmes (Rice), D. Werner (FU Berlin).
Managing Editors: B. G. Bodmann and A. Haynes (Houston)
Houston Journal of Mathematics
Contents
Yuxu Chen, Department of Mathematics, Sichuan University, Chengdu 610064,
China (yuxuchen1210@.sina.com), Hui Kou, Department of Mathematics,
Sichuan University, Chengdu 610064, China (kouhui@scu.edu.cn), and Zhenchao
Lyu, Department of Mathematics, Sichuan University, Chengdu 610064, China
(zhenchaolyu@scu.edu.cn).
Free algebras over continuous spaces, pp. 751–776.
ABSTRACT. Directed spaces are natural topological extensions of dcpos in domain
theory and form a cartesian closed category. A c-space (resp., b-space) can be
characterized as a continuous (resp., algebraic) directed space. We show that continuous
spaces are just all retracts of algebraic spaces through topological ideals, which
are topological generalization of rounded ideals. By means of this result, we
prove the conjecture proposed by Keimel and Lawson in 2012 that the free
algebras over c-spaces are still c-spaces. Besides, we show that the category of
continuous spaces with way-below preserving maps as morphisms is cartesian closed.
Mohammad Ali Parsa, Department of Mathematics, University of Birjand, Birjand,
Iran 97175-615 (mohammadali.parsa@birjand.ac.ir), and Hosein Fazaeli Moghimi,
Department of Mathematics, University of Birjand, Birjand, Iran 97175-615
(hfazaeli@birjand.ac.ir).
Sobrification of modules with I-adic topology, pp. 777–798.
ABSTRACT. Let R be a commutative ring with identity and M be an R-module. For
any ideal I of R, the I-adic sobrification of M denoted sIM, consists of the closure of
elements of M for the I-adic topology on M. This article presents an algebraic theory for
I-adic sobrification of modules. For this purpose, we show that sIR admits
naturally a topological ring structure which can be embedded in the I-adic
completion 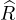 I of R. Moreover, sIM admits naturally a sIR-module structure,
and in particular, sI can be viewed as an additive covariant functor from the
category of R-modules to the category of sIR-modules. Considering I a sequential
ideal (as a new type of ideal) of a Noetherian ring R, it is shown that sI is
naturally isomorphic to sIR ⊗− on finitely generated R-modules. We also study
the left derived functors {LnsI}n∈ℕ of sI, and show that if R is an Artinian
ring, then LnsI(M) is isomorphic to Hn(Mic(Xi ⊗ M)) as the n-th homology
of the microscope complex Mic(Xi ⊗ M) with Xi a free resolution of R∕Ii.
I of R. Moreover, sIM admits naturally a sIR-module structure,
and in particular, sI can be viewed as an additive covariant functor from the
category of R-modules to the category of sIR-modules. Considering I a sequential
ideal (as a new type of ideal) of a Noetherian ring R, it is shown that sI is
naturally isomorphic to sIR ⊗− on finitely generated R-modules. We also study
the left derived functors {LnsI}n∈ℕ of sI, and show that if R is an Artinian
ring, then LnsI(M) is isomorphic to Hn(Mic(Xi ⊗ M)) as the n-th homology
of the microscope complex Mic(Xi ⊗ M) with Xi a free resolution of R∕Ii.
Grigore Călugăreanu, Department of Mathematics, Babeş-Bolyai University,
Cluj-Napoca, 400084, Romania (calu@math.ubbcluj.ro), and Horia F. Pop,
Department of Computer Science, Babeş-Bolyai University, Cluj-Napoca, 400084,
Romania (horia.pop@ubbcluj.ro).
On square stable range one matrices over commutative rings, pp. 799–824.
ABSTRACT. Khurana and Lam introduced the concept of left square stable
range one (ssr1) for an element of a unital ring. In this paper, over commutative rings,
we examine 2 × 2 matrices that satisfy the ssr1 condition. Our findings indicate
significant differences from the stable range one (sr1) condition, necessitating the
development of specialized techniques.
Among our results, we provide characterizations of 2 × 2 matrices that possess ssr1 in
several cases: implicitly over commutative rings, nilpotent matrices over commutative
reduced rings, and explicitly over elementary divisor domains.
As applications, we demonstrate that over commutative Bézout domains, ring
multiples of idempotent 2 × 2 matrices have ssr1. Additionally, we characterize ssr1
matrices with a zero row (or zero column) and offer an explicit description of ssr1
integral matrices.
Building on these results, we further show that the Jacobson Lemma for ssr1 holds for
2 × 2 integral matrices, contingent on a conjecture regarding the greatest common
divisors of their entries.
M.M. Czerwińska, Department of Mathematics and Statistics, University of North
Florida, Jacksonville, FL 32224 (m.czerwinska@unf.edu).
Monotone properties in symmetric spaces of measurable operators, pp. 825–840.
ABSTRACT. Let ℳ be a semifinite von Neumann algebra with a faithful,
normal, semifinite trace τ. We study connections between the monotonicity
properties of an operator x in a noncommutative symmetric space E(ℳ,τ)
and its singular value function μ(x) in a symmetric Banach function space
E on [0,τ(1)). Consequently, we reveal that the monotonic characteristics of
symmetric operator spaces strongly correlate with their convex properties. Moreover,
a new connection is uncovered between the k-extreme points and the upper
monotone points within the framework of symmetric function and operator spaces.
Timothy Rainone, Occidental College, Department of Mathematics, 1600 Campus Rd,
Los Angeles, California, 90041 (trainone@oxy.edu).
C*-norms on cross-sectional algebras and conditional expectations, pp. 841–859.
ABSTRACT. C∗-algebras that arise from groups, dynamical systems, topological
groupoids, and Fell bundles are all constructed as norm completions of convolution, or
rather, cross-sectional algebras. In each of these cases there is a C∗-norm obtained from
the spatial left-regular representation which allows for a natural evaluation map to be
continuous and faithful. The continuous extension of this evaluation map to the
C∗-completion is known as a conditional expectation. In this piece we prove a
fundamental factor lemma and apply it in each of these constructions to show that the
left-regular norm is the smallest C∗-norm making the expectation continuous.
Yingcui Zhao, School of Computer Science and Technology, Dongguan University of
Technology, No.1 Daxue Road, Dongguan City, 523808, Guangdong Province, China
(zycchaos@126.com).
Kato’s chaos of a multiple mapping and its continuous self-map, pp. 861–872.
ABSTRACT. In 2016, Hou and Wang introduced the concept of multiple mappings
based on iterated function system, which is an important branch of fractal theory. In this
paper, we introduce the definitions of sensitivity, accessibility, and Kato’s chaos of
multiple mappings from a set-valued perspective. We show that a multiple mapping and
its continuous self-maps do not imply each other in terms of sensitivity or accessibility.
While a sufficient condition for multiple mappings to be sensitive, accessible and
Kato’s chaotic is provided, respectively. And the sensitivity, accessibility, and
Kato’s chaos of multiple mappings are preserved under topological conjugation.
Runa Shimada, Department of Mathematics, Graduate School of Science, Kobe
University, 1-1 Rokkodai, Nada, Kobe 657-8501, Japan (231s010s@stu.kobe-u.ac.jp).
Geometry on deformations of S1 singularities, pp. 873–890.
ABSTRACT. To study a one parameter deformation of an S1 singularity taking into
consideration its differential geometric properties, we give a form representing the
deformation using only diffeomorphisms on the source and isometries of the target. Using
this form, we study differential geometric properties of S1 singularities and the Whitney
umbrellas appearing in the deformation.
Tongzhu Li, Department of Mathematics, Beijing Institute of Technology, Beijing,
100081, China (litz@bit.edu.cn), and Bingxin Xie, Department of Mathematics, Beijing
Institute of Technology, Beijing, 100081, China (xiebingxinchn@163.com).
Möbius semi-parallel hypersurfaces with three distinct principal curvatures in 𝕊n+1, pp.
891–903.
ABSTRACT. Let x : Mn → 𝕊n+1 be an immersed hypersurface without umbilical points
in an (n + 1)-dimensional sphere 𝕊n+1, one can define two fundamental Möbius
invariants on Mn, the Möbius metric g and the Möbius second fundamental form B. Let
Rm denote the Riemannian curvature operator of the Möbius metric g, the hypersurface
x is called a Möbius semi-parallel hypersurface if Rm ∘B = 0. In this paper, we classify
completely the Möbius semi-parallel hypersurfaces with three distinct principal
curvatures up to a Möbius transformation.
Y. Wang, School of Mathematics and Statistics, Henan Normal University, Xinxiang
453007, Henan, P. R. China (wyn051@163.com).
A classification of real hypersurfaces in nonflat complex space forms, pp. 905–920.
ABSTRACT. In this paper we present a classification theorem of real hypersurfaces in a
nonflat complex space form in terms of the classification of the induced almost contact
metric structures on the hypersurfaces.
Dimitrios Poulakis. Department of Mathematics, Aristotle University of Thessaloniki,
54124 Thessaloniki, Greece (poulakis@math.auth.gr).
On the number of integral points on curves of genus zero, pp. 921–931.
ABSTRACT. Let F(X,Y ) be an absolutely irreducible polynomial in ℤ[X,Y ] such that
the algebraic curve defined by the equation F(X,Y ) = 0 is of genus zero with at
least three infinite valuations. In this note, we compute an improved upper
bound for the number of solutions (x,y) ∈ ℤ2 to the equation F(X,Y ) = 0.
Guodong Hua, School of Mathematics and Statistics, Weinan Normal University,
Weinan, Shaaxi Province, China 714099, Research Institute of Qindong
Mathematics, Weinan Normal University, Weinan, Shaaxi Province, China 714099
(gdhuasdu@163.com).
On higher power moments of coefficients of Dedekind zeta function twisted by Fourier
coefficients of cusp forms, pp. 933–958.
ABSTRACT. Let K3 be a non-normal cubic extension over ℚ, and let aK3(n)
denotes the n-th coefficient of the Dedekind zeta function associated to K3∕ℚ.
Let λg(n) be the n-th normalized Fourier coefficient attached to a primitive
holomorphic cusp form of even integral weight k ≥ 2 for the full modular group
Γ = SL(2, ℤ). In this paper, we investigate the asymptotic behaviour of higher power
moments of aK3(n) twisted by Fourier coefficients of cusp forms of the type
where ℓ1 ≥ 2,ℓ2 ≥ 1 are any given integers. Furthermore, as an application, we also
establish the corresponding asymptotic formula of the variance of aK3ℓ1(n)λg2ℓ2(n).
Jiewen Chen, School of Mathematics and Statistics, Shaanxi Normal University, Xi’an,
Shaanxi 710119, P.R. China (cje1993@163.com), and Bin Zhao, School of Mathematics
and Statistics, Shaanxi Normal University, Xi’an, Shaanxi 710119, P.R. China
(zhaobin@snnu.edu.cn).
Countable type properties in quotient spaces of paratopological groups, pp.
959–975.
ABSTRACT. In this paper, we investigate countable type properties in quotient spaces
of paratopological groups. It is mainly show that if H is a compact subgroup of a
paratopological group G, then (1) G∕H has countable type ⇔ G∕H is feathered ⇔ G
contains a compact subgroup K with H ⊂ K such that χ(K∕H,G∕H) ≤ ω and G∕K is
quasi-metrizable; (2) G∕H is quasi-metrizable ⇔ G∕H is feathered and csf-countable ⇔
G∕H is feathered and has countable tightness ⇔ G∕H is a feathered K-space.
Zheng Ping, Department of Mathematics, Ningde Normal University, Ningde, Fujian
352100, P.R. China (63113015@qq.com), Shou Lin, Institute of Mathematics, Ningde
Normal University, Ningde, Fujian 352100, P.R. China (shoulin60@163.com), and
Rongxin Shen, Department of Mathematics, Taizhou University, Taizhou, Jiangsu
225300, P.R. China (srx20212021@163.com).
αi-Fréchet spaces as the images of metric spaces, pp. 977–992.
ABSTRACT. In this paper we discuss how to represent αi-Fréchet spaces for
i ∈{1,2,3,4} as certain images of metric spaces, and how to characterize a space so that
every quotient mapping onto the space is a pseudo-open-like mapping. It is known that a
space X is an α2-Fréchet (resp., α4-Fréchet) space if and only if it is a strictly countably
bi-quotient (resp., countably bi-quotient) image of a metric space. It is proved that (1)
X is an α1-Fréchet space if and only if it is an α1-sequence-covering and pseudo-open
image of a metric space; (2) X is an α3-Fréchet space if and only if it is an
α3-pseudo-open image of a metric space. We also provide a few examples to show that
some implications do not hold among αi-spaces and αi-Fréchet spaces, and to
illustrate some irreversible relationships among the mappings discussed in this
paper.
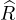 I of R. Moreover, sIM admits naturally a sIR-module structure,
and in particular, sI can be viewed as an additive covariant functor from the
category of R-modules to the category of sIR-modules. Considering I a sequential
ideal (as a new type of ideal) of a Noetherian ring R, it is shown that sI is
naturally isomorphic to sIR ⊗− on finitely generated R-modules. We also study
the left derived functors {LnsI}n∈ℕ of sI, and show that if R is an Artinian
ring, then LnsI(M) is isomorphic to Hn(Mic(Xi ⊗ M)) as the n-th homology
of the microscope complex Mic(Xi ⊗ M) with Xi a free resolution of R∕Ii.
I of R. Moreover, sIM admits naturally a sIR-module structure,
and in particular, sI can be viewed as an additive covariant functor from the
category of R-modules to the category of sIR-modules. Considering I a sequential
ideal (as a new type of ideal) of a Noetherian ring R, it is shown that sI is
naturally isomorphic to sIR ⊗− on finitely generated R-modules. We also study
the left derived functors {LnsI}n∈ℕ of sI, and show that if R is an Artinian
ring, then LnsI(M) is isomorphic to Hn(Mic(Xi ⊗ M)) as the n-th homology
of the microscope complex Mic(Xi ⊗ M) with Xi a free resolution of R∕Ii.